The Bayesian way to the raven paradox (I): systematic inference • Adapting's Blog

This is a mathematical formalisation of the solution to the raven paradox via an introduction to Bayesian inference. See section 1. of this previous post for a brief statement of the paradox.

1. Presenting the tool: Bayes’ rule

Bayes’ rule is a fundamental statistical result that is key to evaluating and adjusting models. If the word “model” doesn’t say much to you, you can think of “hypothesis” instead; hence this rule is fundamental to scientific inquiry (based on hypothesis testing¹) and more generally to extracting knowledge from data.

The key to these tasks is to note that a hypothesis is essentially a model of how certain data are expected to turn out. In mathematical terms, what we have is the probability distribution ( $P$ ) of the data ( $D$ ) given our hypothesis ( $H$ ), represented as $P(D|H)$ . This may come in handy when we want to make predictions about future outcomes, but that’s not our current concern, we want to validate our hypothesis (assess how likely it is) or in other words, find the probability of our hypothesis given the data $P(H|D)$ ², which is in some way the reverse of what we have.

And this is what Bayes’ rule lets us do. You can just see that the probability of two events $X$ and $Y$ , $P(X, Y)$ , can be expressed in two different but equivalent ways: either the probability of $X$ , $P(X)$ , times the probability of $Y$ given $X$ , $P(Y|X)$ , or the probability of $Y$ , $P(Y)$ , times the probability of $X$ given $Y$ , $P(X|Y)$ ³. Then we just have to rearrange terms to get our reversal rule:

\begin{align*}\tag{1} P(X,Y) =& P(X)P(Y|X) = P(Y)P(X|Y), \\[5mm] P(Y|X) =& \frac{P(X|Y)P(Y)}{P(X)}. \tag{2} \end{align*}

So it turns out that in order to revert $P(D|H)$ into $P(H|D)$ we need:

$P(H)$ : the probability we assign to our hypothesis before seeing the data, which would be based either on earlier data or theoretical models.
$P(D)$ : the probability of seeing the data we actually saw. This term can be more problematic, but sometimes one can do without it; more on this later.

Now since examples are often more helpful than just plain discussion and anyway we came here to address the raven paradox, let’s start considering how all of this would play out in our case.

2. Modelling inference in the raven paradox

2.1 Set up

Recall that we have the following proposition that we want to prove/assess empirically:

$B$ : all ravens are black.

First we will consider the case where we are growing increasingly more confident after seeing a number $n$ of black ravens (we denote any instance of seeing a distinct black raven $b_i$ ). So $B$ we will be our hypothesis (formerly $H$ ) and the observations $b_1, b_2, ..., b_n$ will be our data (formerly $D$ ). Following Bayes’ rule we have:

\begin{equation*}\tag{3} P(B | b_1, b_2, ..., b_n) = \frac{P(b_1, b_2, ..., b_n | B) | P(B)}{P(b_1, b_2, ..., b_n)}. \end{equation*}

Our purpose was to understand the term on the left, and we will do so by unpacking the terms on the right, as they are more approachable. Starting with the numerator, we have the probability of multiple events happening (the observations $b_1, b_2, ..., b_n$ ) and would like to break it down into the probability of each event. Intuitively, the total probability is the combination of the probability of each observation conditioned on all the previous observations up to that point. Formally, this unwinding is called the chain rule and goes as follows:

\begin{align*}\tag{4} P(b_1, b_2,& ..., b_n | B) =\\ &P( b_1 | B)P( b_2 | B, b_1) ... P(b_n |B, b_1, b_2, ..., b_{n-1}). \end{align*}

This is particularly relevant when the events are not independent among themselves, so for instance, if you are drawing cards from a deck (without replacement), for each consecutive time from the start that you haven’t drawn (let’s say) the ace of diamonds, it becomes more likely that you’ll draw it in the next time.

All the terms of the sort $P(b_i | B, ...)$ are 1, since all ravens being black ( $B$ ) guarantees the next raven we see will be black⁴. Thus, the fraction simplifies to:

\begin{equation*}\tag{5} P(B | b_1, b_2, ..., b_n) = \frac{P(B)}{P(b_1, b_2, ..., b_n)}. \end{equation*}

Notice that since probabilitites are less or equal to 1, we get $P(B | b_1, b_2, ..., b_n) \geq P(B)$ (because $P(b_1, b_2, ..., b_n) \leq 1$ ), that is, the probability of all ravens being black gets higher as we see more black ravens (without seeing non-black ravens) as expected.

Recall that $P(B)$ is the prior probability, which is based either on previous data, technical knowledge, theoretical intuition or beliefs. For the sake of simplicity (no need to be rigorous here, after all we are formalising the raven paradox and these sort of details have no impact in its core propositions) we could say that it is not very likely that a bird species is completely black and so we can give it 10% probability: $P(B) = 0.1$ ⁵. Now all we need to calculate is $P(b_1, b_2, ..., b_n)$ , the probability of having seen $n$ black ravens.

This term is often problematic and can be bypassed in certain cases, but here we will just rely on making further specifications. Since we are more comfortable with conditional probabilities, we can try to expand it into the probability of seeing such $n$ black ravens under every possible hypothesis times the probability of that hypothesis. We could say there’s only one alternative to all ravens being black ( $B$ ) and that is not all ravens being black (named $B^c$ onwards) so we would have:

\begin{align*} P(b_1, b_2,& ..., b_n) = \\ &P(b_1, b_2, ..., b_n | B)P(B) + P(b_1, b_2, ..., b_n | B^c)P(B^c),\tag{6} \end{align*}

Recall that the conditional probability under $B$ is just 1 and that since $B^c$ is the complement (complement is just the probability term for opposite) of $B$ we have $P(B^c) = 1 - P(B)$ . Hence we have arrived at:

\begin{equation*}\tag{7} P(B | b_1, b_2, ..., b_n) = \frac{P(B)}{P(B) + P(b_1, b_2, ..., b_n | B^c)(1 - P(B))}. \end{equation*}

Still we have one piece missing, namely $P(b_1, b_2, ..., b_n | B^c)$ , which is basically the model that represents how the alternative hypothesis⁶ $B^c$ looks like. This is not going to be as easy as the model for $B$ , but sometimes more difficult means more interesting, and here a little bit of complication will allow for a deeper discussion of Bayesian modelling.

2.2 Modelling the complement

The main issue with the complement is that there are many different ways of not all ravens being black: is it just one that is not black?, is it all of them that are not black?, or anything in between? We will address this by giving a certain amount of probability to each possible case. But let’s first take a look at what would happen if we were sure that the only posibble cases where extreme cases, so that we can check whether what we’ve got so far makes sense.

Suppose that for some reason we know ravens are monochromatic, so they are either all black ( $B$ ) or non-black ( $B^c$ ), meaning:

P(b_1, b_2, ..., b_n | B^c) = 0

Substituting in (7) we get:

P(B | b_1, b_2, ..., b_n) = \frac{P(B)}{P(B)} = 1.

Expectedly, the probability of all ravens being black is 1 after seeing any number of black ravens, in fact a single black raven would suffice.

The other extreme is even less plausible but let’s consider it anyway. Suppose we were certain that either all ravens are black ( $B$ ) or a single one of them is not black ( $B^c$ ). Then $B$ would be hardest to prove, as for a high enough number of ravens, we would have that all ravens being black and all but one being black are almost equivalent, leading to:

P(b_1, b_2, ..., b_n | B^c) \simeq 1.

If we substitue in (7):

P(B | b_1, b_2, ..., b_n) \simeq \frac{P(B)}{P(B) + 1 - P(B)} = P(B)

Thus seeing any number of black ravens is irrelevant (our prior does not get updated) because both possibilities under consideration are essentially the same (i.e., seeing a non-black raven is practically impossible).

All good so far, it seems like (7) is doing the job, so let’s come back to the more realistic case then. For that, we will name the number of ravens $n_r$ and the number of black ravens $n_b$ . For now let’s consider $n_r$ is known⁷ and let’s model the uncertainty that we have as to what the actual value of $n_b$ is through a probability distribution. This is easier to do considering the two hypothesis separately. First, by definition we have $P(n_b=n_r | B) = 1$ (that is the formalization of “all ravens are black”), which also implies $P(n_b=k | B) = 0$ for any $k < n_r$ . So what we really have to model is the probability of there being $k$ black ravens under the alternative hypothesis $B^c$ . If we consider, for instance, each value equally likely, we would have⁸:

\begin{equation*}\tag{8} P(n_b = k | B^c) = \frac{1}{n_r}, \; (0 \leq k \leq n_r-1). \end{equation*}

Now we can get $P(b_1, b_2, ..., b_n | B^c)$ . The key here is that we can get this probability for a given amount of black ravens $n_b=k$ , and then we can average out across all posible values of $n_b$ according to their probability $P(n_b=k | B^c)$ . In mathematical terms:

\begin{equation*}\tag{9} P(b_1, b_2, ..., b_n | B^c) = \sum_{k=0}^{n_r-1} P(b_1, b_2, ..., b_n | n_b = k) P(n_b = k | B^c). \end{equation*}

It’s a little bit as if the term $n_b = k$ is cancellating out⁹.

Since we have already defined $P(n_b = k | B^c)$ we bring our attention to the other term $P(b_1, b_2, ..., b_n | n_b = k)$ which represents a process analogous to that of drawing cards from a deck (each one we draw modifies the probability of drawing the next). To make the derivation of this probability more explicit, let’s use the chain rule to split it into individual steps:

\begin{align*} &P(b_1, b_2, ..., b_n | n_b=k) = \\ &\quad P( b_1 | n_b=k)P( b_2 | n_b=k, b_1) \; ... \; P(b_n | n_b=k, b_1, b_2, ..., b_{n-1}). \quad \tag{10} \end{align*}

For each step the probability of getting a black raven is just the ratio between black ravens and total ravens, but notice that as we make more “drawings” these sets decrease:

\begin{align*} P( b_1 | n_b=k) &= \frac{k}{n_r}, \quad P( b_2 | n_b=k, b_1) = \frac{k - 1}{n_r - 1}, \quad ..., \\ &P( b_n | B^c, b_1, b_2, ..., b_{n-1}) = \frac{k - n}{n_r - n}. \tag{11} \end{align*}

As we “draw” more black ravens, it becomes less likely that the next raven will be black until $n=k$ where it becomes 0. At that point the calculation should stop, as goind beyond has no physical meaning. Hence we would only use (11) for $n < k$ , otherwise $P( b_1, b_2, ..., b_n | n_b=k) = 0$ .

Now we can subsitute in (10) and bring all the terms together using product notation:

\begin{equation*}\tag{12} P(b_1, b_2, ..., b_n | n_b=k) = \prod_{i=0}^{n-1} \left( \frac{k-i}{n_r-i} \right), \end{equation*}

and it’s the probability weighted average of this value that we are looking for (we will move the term $P(n_b=k | B^c)$ to the left to make it explicit that it does not take part in the product):

\begin{equation*}\tag{13} P(b_1, b_2, ..., b_n | B^c) = \sum_{k=0}^{n_r-1} P(n_b = k | B^c) \prod_{i=0}^{n-1} \left( \frac{k-i}{n_r-i} \right). \end{equation*}

Now replacing in (7):

\begin{align*} P(B& | b_1, b_2, ..., b_n) = \frac{P(B)}{P(B) + P(b_1, b_2, ..., b_n | B^c)(1 - P(B))} = \\ & \frac{P(B)}{P(B) + (1 - P(B)) \sum_{k=0}^{n_r-1} P(n_b = k | B^c) \prod_{i=0}^{n-1} \left( \frac{k-i}{n_r-i} \right)}, \tag{14} \end{align*}

and we are done! Unfortunately at this point we have reached high enough complexity for the expression to be hard to interpret as it is. However, we do have a way to calculate the probabilities we were looking for, so let’s follow the experimental approach plugging in some numbers for our variables (which are $n_r$ and $n$ ) and see what we get.

2.3 Experiments

We will consider a total population of 1000 ravens ( $n_r=1000$ )¹⁰, starting from a prior probability that all ravens are black of 0.1 ( $P(B) = 0.1$ ) and we will see how our probability updates after seeing the first 200 ravens (which represent 20% of the total population) for two different alternative hypothesis (characterized by different probability distributions over $n_b$ ).

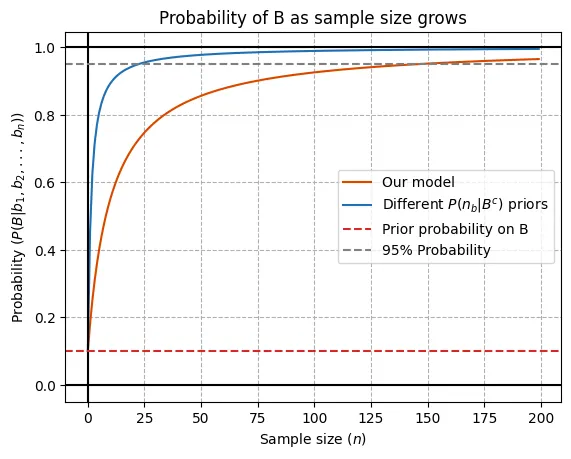
Let’s first focus on the orange line which corresponds to the model we’ve been discussing so far. Starting from our reasonably skeptical prior of 10%, the probability of all ravens being black increases rapidly and around 30 black raven observations suffice to reach an 80%. Growth gradually slows down, reaching 95% probability with 150 observations and converging asymptotically towards 100% (which is only exactly reached with 1000 observations).

If you are wondering about the blue line, it’s practically the same model, but using a different prior over the number of black ravens under the alternative. Recall we were using a flat prior $P(n_b=k |B^c) = \frac{1}{n_r}$ which, as discussed⁸, implies a heavy bias towards the existence of black ravens. We therefore also consider a more balanced approach by putting higher probabilities on smaller numbers of black ravens, more specifically we set $P(n_b=k | B^c) \propto \frac{1}{1 + k}$ ¹¹. Perhaps the difference between these two configurations can be appreciated more easily in the following plot.

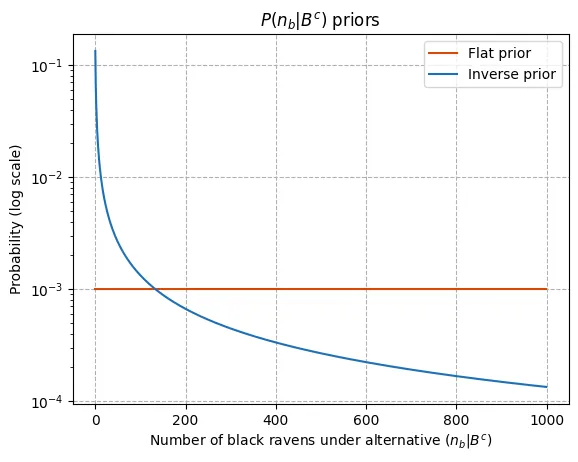
Going back to the probability updates graph, we see that the probability for $B$ under the blue model grows much quicker, why is so? Well, in this case, under $B^c$ we have assigned more probability to the number of black ravens being low, so any instance of seeing a black raven is far worse explained by $B^c$ , hence the placing of stronger belief on $B$ . Note that here 25 observations suffice to reach 95% probability!

A note on the speed of updating and the power of randomness

If you found the speed of these updates (not only for the blue but also the orange model) a little surprising, you are not alone; it seems odd that very few data is enough to build such strong beliefs. Nonetheless it’s possible to make sense of both the fact that this result is so and that it appears as counterintuitive.

First, another potentially counterintuitive (but hopefully illuminating) result. Let’s consider the degree to which different values of $n_b$ can be consistent with having observed 25 consecutive black ravens. For instance, if there where 900 black ravens, ( $n_b = 900$ ), which is a value that doesn’t seem so far off from $B$ (where we would have $n_b = 1000$ ), the probability of having had such observations would have been 7% (you can get a quick upper bound by doing $\left(\frac{900}{1000}\right)^{25}$ ). So values smaller than 900, which constitute most of the $B^c$ hypothesis (at least with the flat priors and even more so with the inverse ones), are rather poor at explaining the data, therefore dragging the probability of $B^c$ down fairly quickly. The value of 50% probability is only reached after $n_b = 973$ , and we are talking about just 25 observations! Okay, so this tells us that the model updating speed is not that unreasonable after all, but why is again everything so counterintuitive?

The key difference between this problem and the kind of problems our intuition was built for is random/independent sampling. Throughout this post we have assumed that the observations of black ravens were independent among themselves (once again, because this simplifies calculations and has no impact on the discussion of the raven paradox). However, can you imagine observing ravens independently? In the real world, most of the samples we observe (or at least those that our ancestors observed during the evolutionary period along which our intuition developed) are both spatially and temporally correlated; for instance, we see a group of ravens flying together, or our observations are limited to some corner of the world¹². Correlation means that the individuals share some amount of information, which in turn means that the whole is less informative than the sum of the information contained in the individuals. In the extreme case of 100% correlation, a single individual contains the same information as any number of them (100% correlation can be thought of as implying they are identical copies).

So our intuition is not wrong after all, it’s just build for more historically realistic scenarios (“historically realistic” because modern technology makes it increasingly more possible to achieve quasirandom sampling, although it’s still something we do not encounter in our day to day lives for the most part). This small digression serves to highlight the importance of random sampling (or limiting samples correlation) to maximize the amount of information obtained per individual; in fact, it’s not casuality that this a foundational principle in scientific experimental design or in conducting surveys¹³.

3. Wrapping up

We’ve developed a model for assessing the probability of all ravens being black, but we still need a model to assess the contrapositive in order to close our Bayesian formalization of the raven paradox. We will see this is quite straightforward but, since we’ve come a long way already and there are still some interesting results ahead that will require some explanation, this looks like a nice place to stop. Besides, the Bayesian framework presented above for hypotheses/models’ evaluation is already valuable in itself (arguably much more so than solving the paradox, although perhaps less entertaining) so it’s certainly worth a post of its own. Anyway, if you are interested in seeing how this all continues, you can read more here.

Footnotes

A comment on this for those already familiar with statistics (which is another way to say that if you do not understand what follows, you shouldn’t worry). Here “hypothesis testing” is not used in the specific statistical sense (often linked to frequentism) but in a broader sense as in “hypothesis assessment”. So why not just use the second unequivocal term and avoid the need for clarification? The underlying claim in here is that the two terms should be equivalent, and the fact that the first has acquired a whole new layer of meaning has to do with a certain tendency within statistics to needlessly complicate and obscure rather intuitive concepts. ↩
Similarly if we are just concerned with parameter estimation, denoting the parameters $\theta$ we would have $P(D|\theta, H)$ and we would be looking for $P(\theta | D, H)$ . Anyway, the difference between model and parameter is not very relevant here, as two distinct models can be subsumed within a larger model where they are expressed as two distinct sets of parameters. ↩
You may recall that the probability of two independent events $X$ , $Y$ is obtained by multiplying their respective probabilities: $P(X,Y) = P(X)P(Y)$ . This is just a concrete case of the more general formulation in (1): note that independence means that knowing one variable’s value tells nothing about the other so $P(X|Y) = P(X)$ and then $P(X,Y) = P(X)P(Y|X) = P(X)P(Y)$ . ↩
Yes, we could have reached this conclusion just by inspecting $P(b_1, b_2, ..., b_n | B)$ . However, generally we won’t be that lucky and the chain rule is a fundamental tool for manipulating probabilities (which we will need further along this post) so we considered worth it taking the long route in this case. ↩
In what way is this a simplification? Making $P(B) = 0.1$ is kind of saying we are 100% sure that our belief is 10% probability; but it is more common to be uncertain about our own estimate. This would be represented by placing a probability distribution over our prior (yes, it would be a probability distribution over probabilities). This means our model would no longer be about $P(B)$ but about $P(P(B))$ if you will, which may seem convoluted (and certainly here we are ignoring it in favor of clarity) but it often yields more accurate representations of real world uncertainty. ↩
Again, here “alternative hypothesis” should not be interpreted in the common statistical sense but in a more general one. Don’t worry if this makes no difference to you. ↩
Clearly knowing the number of ravens in advance is not very realistic but we will ignore it because it adds another layer complexity without having relevant implications for our discussion. We leave some brief comments in case you are interested but they are probably better undestood after reading the rest of the post. As we will do with the parameter $n_b$ , the way to model this uncertainty would be with a probability distribution, which means assigning a probability to each possible value $n_r$ can have (let’s say we estimate anything between a hundred thousand and a hundred million is equally likely). Then, since we will already know how to get our desired results for any value of $n_r$ (after getting to end of the post, that is), we will be able to do so for every possible number of ravens and average out the output, weighting each instance according to its probability. It would look something like this: $P(B | b_1, b2, ..., b_n) = \sum_{n_r} P(B | b_1, b_2, ..., b_n, n_r) P(n_r)$ . ↩
Note that although it seems like we have made a rather impartial choice, in actuality the model is heavily biased towards the prospect of ravens being black. The expected number of black ravens under the alternative is $\mathrm{E}[n_b|B^c] = \frac{n_r - 1}{2}$ . This is because we have parametrized the problem in terms of ravens being black vs non-black, so a presumably impartial assignment of probability implies considering black as likely as all other colors (and their combinations) combined. Once again, we will not bother much about this (we will consider a less biased distribution though) because it doesn’t affect the purpose of our discussion; but it serves to highlight the importance of being aware of how the definition of the variables needs to be carefully considered when choosing priors over parameters so as not to inadvertedly introduce strong biases. ↩ ↩²
The main process through which variables “disappear” (or “appear” when we follow the opposite direction) in probability is called marginalization and can be summarised as: $\sum_z P(x,z) = P(x)$ . In words, considering the joint probability of $x$ and $z$ , $P(x,z)$ , over every possible value of $z$ amounts to the probability of $x$ . Recalling $P(x,z) = P(x|z)P(z)$ we can then get: $P(x) = \sum_z P(x,z) = \sum_z P(x|z)P(z)$ . What we’ve done in (9) is the same thing but conditioning every probability on $B^c$ , something like $P(x|y) = \sum_z P(x|z, y)P(z | y)$ . The only reason we didn’t write $P(b_1, b_2, ..., b_n | n_b = k, B^c)$ is because the fact that $n_b=k$ for $k < n_r$ already implies $B^c$ so it’s somewhat redundant. ↩
Clearly there are more than 1000 ravens on Earth (apparently 16 million according to Wikipedia); however we wanted to keep the size small because it’s more convenient for practical matters. More specifically: one can write quick code without the need to worry about precision errors, memory handling or execution time (consider that later on when we take on the contrapositive we would have population sizes of something like $10^25$ non-black things if we wanted to be realistic). Besides this has no impact for the purposes of discussing the paradox or inference. ↩
We only care about proportionality (denoted by $\propto$ ) because the normalization constant is determined by the fact that probabilities should add up to 1, that is, we have the following constraint: $\sum_{k=0}^{n_r-1} P(n_b = k | B^c) = 1$ . ↩
A very handy example since we are dealing with the colors of birds: up to 1697 Europeans believed all swans to be white, then Dutch mariners found black swans in Australia. ↩
Note the connection between randomness and information. This is one of the doorways to the notion of entropy (the other being the classical thermodynamic interpretation that is much more difficult to grasp) and leads to a very interesting discussion of the concept, but we will leave that for another post. ↩